Vielleicht liegt es an der merkwürdigen Corona-Zeit — auf jeden Fall hatte ich in den letzten Wochen eine Phase, in der ich fast täglich Sudokus löste. (Meine Quelle: https://www.derstandard.at/lifestyle/raetsel-sudoku.) Die Sudoku-Sucht hat schon wieder nachgelassen, aber Programmierer der ich nun einmal bin, fand sich gleich die nächste Herausforderung: Es kann doch nicht so schwierig sein, ein Programm zu schreiben, das Sudokus löst — oder? Natürlich weiß ich, das Internet ist voller Sudoku Solver. Es ging mir keineswegs darum, das Rad neu zu erfinden oder es noch runder zu machen — ich hatte einfach Lust auf ein paar Stunden Programmieren. Just for fun, nicht als Beispiel für ein Buch oder für den Unterricht …
Gesagt, getan. Wegen der Arbeit an meinem Kotlin-Buch ist mir die Sprache gerade sehr vertraut. Nach ein paar Stunden konnte mein Code bereits einfache Sudokus lösen. Der letzte Feinschliff dauerte dann doch etwas länger als gedacht, aber mittlerweile glaube ich, dass das Programm zuverlässig funktioniert.
Und weil es schade wäre, das fertige Programm nun einfach wieder in der Versenkung verschwinden zu lassen, habe ich es auf GitHub gestellt. Dieser Artikel dokumentiert kurz die Funktionsweise.
Programmaufbau
Der gesamte interessante Code befindet sich in der Klasse Sudoku. Diese ist wie folgt anzuwenden:
val test = """
3192.....
......7.1
...63....
67.8.35..
9.......3
..21.5.47
....62...
2.3......
.....7259
""".trimIndent()
val sudoku = Sudoku(test)
sudoku.plot() // plot unsolved Sudoku
println(sudoku.solveRecursive())
sudoku.plot() // plot solution
Der Konstruktor von Sudoku erwartet eine Zeichenkette, die in neun Zeilen die Ziffern des Sudokus enthält. Jedes Zeichen, das keine Ziffer ist, gilt als leeres Feld. Der Konstruktor initialisiert die Eigenschaft sudoku, eine verschachtelte Liste aus 9 x 9 Integerzahlen.
Der Schlüssel zur Lösung des Sudokus ist candidates: Dabei handelt es sich um eine weitere 9 x 9 Liste, deren Elemente jeweils ein Set mit allen Zahlen enthalten, die für ein leeres Feld des Sudokus in Frage kommen. Der Konstruktor löscht die Sets für alle bereits belegten Zellen und ruft dann eliminateCandidates auf. Dort werden aus jedem Set alle Zahlen entfernt, die sich in der gleichen Zeile, Spalte oder 3×3-Box befinden. Damit verbleiben die potentiellen Lösungskandidaten.
Die Methode plot gibt das Sudoku am Bildschirm aus. Es greift dabei auf die Klasse ColoredConsole zurück (siehe GitHub), die unkomplizierte Farbausgaben erlaubt.
// Enumeration mit möglichen solve()-Ergebnissen
enum class Result { Finished, Failure, Open; }
// Sudoku-Klasse
class Sudoku(data: String) {
// sudoku: initally empty 9x9 list, to be initalized in constructor
private val sudoku = List(9) { MutableList(9) { 0 } }
// set of candidates for each cell of sudoku
private var candidates =
List(9) { MutableList(9) { mutableSetOf(1, 2, 3, 4, 5, 6, 7, 8, 9) } }
// constructor
init { ...
}
// output current state of Sudoko including solved cells (bold, black)
// and possible candidates (grey)
fun plot(markrow: Int = -1, markcol: Int = -1) { ... }
...
}
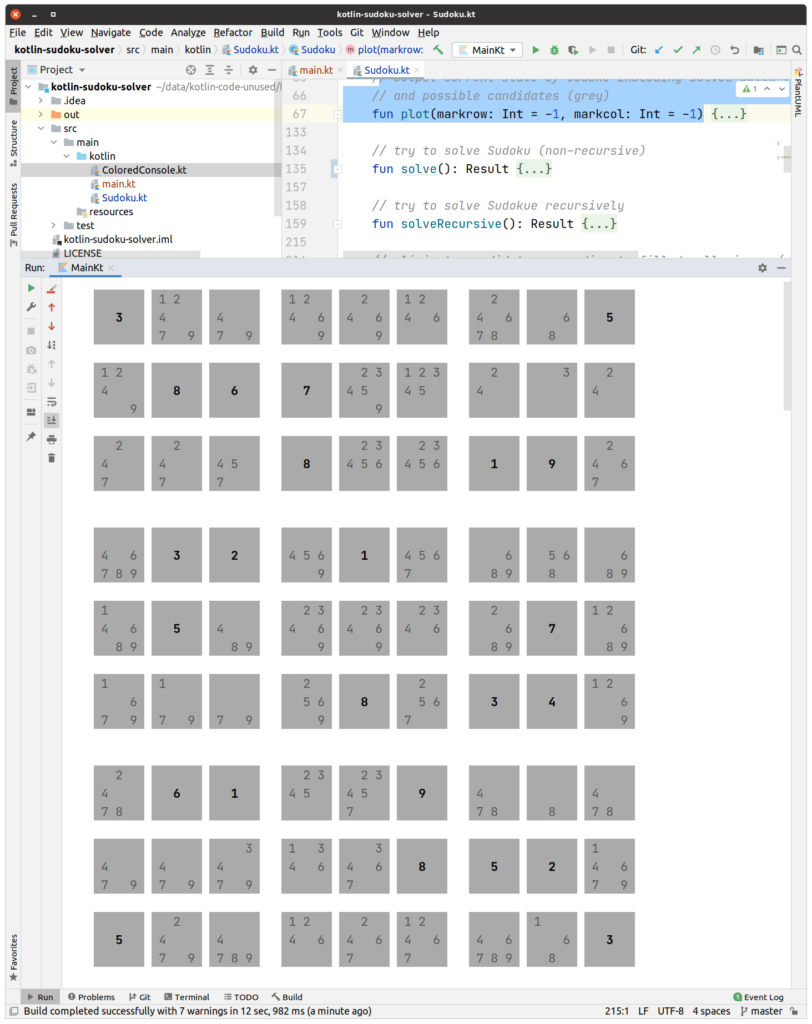
Lösung Teil 1: »Naked Singles«
solve ruft in einer Schleife diverse Methoden auf, die das Sudoku Schritt für Schritt lösen. Die äußere do-while-Schleife endet, wenn keine Fortschritte mehr erzielt werden können.
// try to solve Sudoku (non-recursive)
fun solve(): Result {
do {
val todo = statusCellsOpen
val options = statusCandidatesCount
// call methods repeatedly, until they make no longer progress
do while (findNakedSingle())
do while (findHiddenSingleRow())
do while (findHiddenSingleCol())
do while (findHiddenSingleBox())
// optimize candidate sets
eliminatePairNumbers()
eliminateBoxBlockingNumbers()
// try again, until neither number unsolved sells
// nor number of open candidates drop
} while (statusCellsOpen < todo || statusCandidatesCount < options)
return when {
statusCellsOpen == 0 -> Result.Finished // all done
statusFailedCells > 0 -> Result.Failure // empty cells without candidates
else -> Result.Open // uncertain
}
}
Im ersten Schritt versucht das Programm, alle Naked Singles zu erkennen. Das sind Zellen, für die nur eine einzige Zahl in Frage kommt, weil alle anderen Zahlen in der Zeile, Spalte oder 3×3-Box bereits vorkommen. findNakedSingle durchsucht dazu einfach die Liste candidates nach Sets, die genau ein Element enthalten.
// loop over all candidate sets; if there is a set with exact one item
// set cell accordingly, recalculate candidates and return true;
// else: return false
private fun findNakedSingle(): Boolean {
for (row in 0..8)
for (col in 0..8)
if (candidates[row][col].size == 1) {
val nmb = candidates[row][col].toList()[0]
setCell(row, col, nmb, "Naked Single")
return true
}
return false
}
Wenn findNakedSingle eine passendes Feld findet, wird die entsprechende Zahl in setCell in die Zelle eingetragen. setCell kümmert sich auch darum, die Kandidaten-Sets aller Zellen in der gleichen Zeile, Spalte und 3×3-Box zu aktualisieren. Optional (Variable debugShowPlot) ruft setCell auch plot aus. Damit können Sie dem Programm zusehen, wie es Schritt für Schritt das Sudoku löst. (Die jeweils zuletzt ausgefüllte Zelle wird rot markiert.)

Lösung Teil 2: »Hidden Singles«
Sobald solve keine Naked Singles mehr findet, geht es auf die Suche nach Hidden Singles. Dieser Begriff bezeichnet den Fall, dass es in einer Zeile, einer Spalte oder einer 3×3-Box nur eine einzige Zelle gibt, in der eine bestimmte Zahl in Frage kommt. Die drei Methoden findHiddenSingleRow, findHiddenSingleCol und findHiddenSingleBox suchen nach solchen Zellen.

Lösung Teil 3: Paarweise Eliminierung
Direkt lassen sich jetzt keine Lösungszellen mehr finden. Es gibt aber noch Wege, die Kandidatensets zu minimieren. Das erste Verfahren besteht darin, in einer Zeile, einer Spalte oder einer 3×3-Box zwei identische Zahlenpaare zu suchen. In diesem Fall muss eine Zelle die eine Zahl aufnehmen, die andere Zelle die andere Zahl. Wir wissen aktuell noch nicht, welche Zahl in welcher Zelle landet — sicher ist aber, dass die betreffenden Zahlen in den verbleibenden Zellen der Zeile/Spalte/Box eliminiert werden können! Im Code kümmert sich die Methode eliminatePairNumbers genau darum.

Lösung Teil 4: Box-Eliminierung
Ein weiteres Eliminiationsverfahren sieht so aus: Sie durchsuchen alle 3×3-Boxen, ob es dort eine Zahl gibt, die sicher in genau einer Zeile oder Spalte platziert werden muss. Auch wenn unklar ist, wo die Zahl genau landet — sicher ist, dass diese Zahl dann in den restlichen Zellen anderer Boxen der gleichen Zeile/Spalte nicht sein kann! Der entsprechende Code in eliminateBoxBlockingNumbers ist schon etwas komplizierter und greift auf diverse Hilfsfunktionen zurück (boxBlockAllInSameRow, boxBlockAllInSameCol, boxBlockAllInSameCol und boxBlockEliminateNumberInCol).

Sofern die beiden Eliminiationsverfahren die Anzahl der Lösungskandidaten reduziert haben, besteht eine gute Chance, dass es jetzt wieder Hidden oder Naked Singles gibt. solve beginnt deswegen in einer Schleife von vorne und sucht neuerlich nach Zellen, die jetzt eindeutig sind.
Lösung Teil 5: Versuch und Irrtum (sprich: Rekursion)
Bis einschließlich Teil 4 komme ich normalerweise, wenn ich Sudokus manuell löse. Bei schwierigen Sudokus kommt nun der Punkt, wo Logik nicht mehr weiter hilft: Man muss eine von zwei möglichen Varianten ausprobieren und im Kopf oder mit Stift und Papier herausfinden, ob es so weiter geht oder nicht. Ich gebe da in der Regel auf …
Für das Programm kommt Aufgeben aber natürlich nicht in Frage: solveRecursive ruft zuerst einmal solve auf, um das Sudoku so weit wie möglich zu lösen. Dann sucht es in den verbleibenden Kandidaten-Sets eines mit möglichst wenig Varianten aus. In der Praxis ist das fast immer ein Zweier-Set. Wenn Sie dem Programm ein vollkommen leeres Sudoku zur Lösung geben, dann muss es aber bei einem Neuner-Set zu raten beginnen.
Vom ausgewählten Set wählt das Programm die erste Variante, setzt die Zahl ins Sudoku ein und ruft nun wieder solveRecursive auf. Im Idealfall führt solve nun direkt zur Lösung — oder aber zu einem unlösbaren Sudoku. (Dieses ist erkennbar, weil es Zellen gibt, deren Kandidaten-Set leer ist.) Bei schwierigen Sudokus kann es aber auch passieren, dass es neuerlich keine »logische« Lösung gibt, dass der einzige Fortschritt wieder nur durch Probieren erzielt werden kann.
Bei meinen Tests hat der rekursive Algorithmus immer eine Lösung gefunden, wo eine existiert. Das Programm verschluckt sich auch nicht an Sudokus mit vielen Lösungsmöglichkeiten und liefert dann eben die (aus Sicht des Programms) erste.
Schlussbemerkungen
Mein Ziel mit der obigen Beschreibung war es, Sie so neugierig zu machen, dass Sie Lust verspüren, selbst einen Blick in den Code zu werfen. Den finden Sie auf GitHub.
Ich habe mich bemüht, den Code »lesbar« zu schreiben und in möglichst viele Einzelteile (Methoden) zu zerlegen. Der Code ist allerdings nicht auf Geschwindigkeit optimiert. Das ist auch gar nicht notwendig — er liefert die Lösung sowieso in Sekundenbruchteilen.

Hallo Herr Kofler,
vielen Dank für das tolle Beispiel.
Ich habe vor 25 Jahren mal ein Patience Kartenspiel als Shareware veröffentlicht. Ihr Beispiel hat mich auf Kotlin neugierig gemacht und ich habe mir direkt das Buch gekauft. Ich werde nun, zu Lernzwecken, die Patience als Konlosenprogramm umsetzen.
Danke für die Inspiration!